Cohesive Subgroup
One of the major concerns of social network research is discovery of cohesive subgroups of members within a network. Cohesive subgroups are subsets of members(nodes) among whom there are relatively strong, direct, intense frequent or positive tie. This is not formal but intuitive notion of social group using social network properties. However, since the concept of social group is quite general, and there are many specific properties of a social network that are related to the cohesiveness of subgroups, there are many interesting social network subgroup definitions. (E.g., clique, clan, club, core, plex, etc.)
In my think, the motivation for studying cohesive subgroups in social networks is that we maybe discover lots of meaningful query type with them. In the past, many researchers in physics and social economics have already discussed about the meaning of social cohesion in social explanation and theories (Burt 1984;Collins 1988; Erickson 1988; Friedkin 1984). They said that “Cohesive subgroups are theoretically important because of social forces operating through direct contact among subgroup members, through indirect conduct transmitted via intermediaries, or through the relative cohesion within compared to out side the subgroup.
In computer science fields, (…especially.., database area) we focus on social network as a novel and invaluable data dissemination paradigm. (I’m not sure how dare I could use this expression…. , Actually, I’m just a humble student.) By the way, I describe about some of cohesive group theory in this article.
There are four general properties of cohesive subgroup as following:
- The mutuality of ties
- The closeness or reachability of subgroup members
- The frequency of ties among member
- The relative frequency of ties among subgroup members compared to non-members
Subgroups based on mutuality that all pairs of subgroups members link each other (i.e., all adjacent); subgroups based on reachability require that all all subgroup members could reach to each other, but do necessarily adjacent; subgroups based on numerous ties require that subgroup members have links to many(enough) other within the subgroup; subgroups based on the relatively density or frequency of links require that subgroups be relatively cohesive than remainder of the network
1. Clique
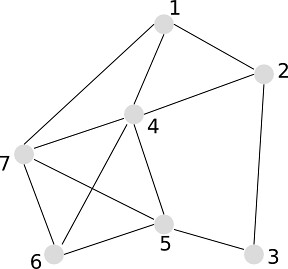
A clique in a graph is a maximal complete subgraph of three or more nodes. In the following graph, {1,2,4},{1,4,7}, and {4,5,6,7} are cliques
2. n-Clique
A n-clique is a maximal subgraph in which the largest distance between any two nodes in no greater than n. In other words, all the member are linked within n-distance. In the following graph {1,2,3,4,5} and {2,3,4,5,6} could be a 2-clique.
3. k-plexes
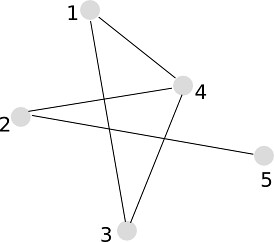
A k-plex is a maximal subgraph containing l nodes in which each node is adjacent to no fewer than (l – k) nodes in the subgraph. Namely, we could omit the k number of links. The following graph represent 2-plex.
– A lot of information in this article is quoted from ‘Social Network Analysis – Method and Applications’ (CAMBRIDGE)

Recent Comments